平稳是随机过程中一个非常重要的概念,而宽平稳则属于其中一种类型。宽平稳过程具有良好的性质,本文首先介绍了其定义,然后研究了宽平稳过程在时域中的性质。本文属于随机过程笔记,根据清华大学电子工程系张颢副研究员的随机过程线上课程笔记整理而成,这是课程链接。
宽平稳过程的概念
随机过程有中一个非常重要的概念:平稳(Stationary)。指随机过程的某一类统计性质随时间变化保持不变,具体是怎样的性质,就需要具体案例具体分析了。
现在介绍宽平稳过程(wide-sense stationary process, W.S.S.)这样一个案例。
定义:若随机过程\(\mathbb{X}(t)\)满足:
不同的时刻\(t\)下,\(\mathbb{X}(t)\)的均值保持不变,即 \[ E\left( \mathbb{X}(t) \right) =m(t) \equiv m \]
对于任意的平移时间\(D\),都有 \[ R_{\mathbb{X}} (t+D,s+D) = R_{\mathbb{X}} (t,s) \]
则称\(\mathbb{X}(t)\)是宽平稳过程。
根据定义的第二条,宽平稳下的随机过程相关函数实际上可以退化成一元函数: \[ \begin{eqnarray} R_\mathbb{X}(t, s) & = & R_\mathbb{X}(t-s, s-s)\\ & = & R_\mathbb{X}(t-s, 0)\\ & \overset{\Delta}{=} & R_\mathbb{X}(\tau) \end{eqnarray} \] 其中,\(\tau = t-s\),即函数值只于\(t,s\)的间距有关,与它们的具体值无关。
下面我们看两个例子。
调制信号 Modulated Signal
设有一随机过程\(\mathbb{X}(t) = A(t)\cos\left( 2\pi f_0 t +\theta\right)\),其中\(A\)是随机过程,\(\theta\)满足均匀分布\(\theta \sim U(0,2\pi)\),并且\(A, \theta\)独立。那么\(\mathbb{X}\)宽平稳吗?
首先考察宽平稳定义的第一条, \[ \begin{eqnarray} E\left(\mathbb{X}(t)\right) & = & E\left(A(t)\right) E\left(\cos\left( 2\pi f_0 t +\theta\right)\right) \\ & = & E\left(A(t)\right) \int_0^{2\pi} \cos\left( 2\pi f_0 t +\theta\right) \mathrm{d}\theta \\ & \equiv & 0 \end{eqnarray} \] 第一条满足;现考察定义的第二条, \[ \begin{eqnarray} R_{\mathbb{X}} (t+D,s+D) & = & E\left(\mathbb{X}(t+D)\mathbb{X}(s+D)\right) \\ & = & E\left(A(t+D)A(s+D)\right) \cdot E\left(\cos\left( 2\pi f_0 (t+D) +\theta\right) \cos\left( 2\pi f_0 (s+D) +\theta\right) \right) \\ & = & E\left(A(t+D)A(s+D)\right) \cdot \cfrac{1}{2}E\left(\cos\left( 2\pi f_0 (t-s)\right)\right) \\ & = & E\left(A(t+D)A(s+D)\right) \cdot \cfrac{1}{2}E\left(\cos\left( 2\pi f_0 \tau \right)\right) \end{eqnarray} \] 因此,若振幅调制\(A(t)\)是宽平稳的,则整体\(\mathbb{X}(t)\)是宽平稳的。
随机电报信号 Random Telegraph Signal
随机过程\(\mathbb{X}\)于每一时间\(t\)上\(\mathbb{X}(t)\)都在\(\set{1,-1}\)中任意取值,现考察其是否宽平稳。设在\(\left[ s,t \right]\)时间段内,信号切变\(k\)次的概率为 \[ \rho = \cfrac{(\lambda(t-s))^k}{k!}\exp(-\lambda(t-s)) \]
这实际上就是泊松分布(Poisson distribution)。另有 \[ \sum_{k=0}^{\infty} \cfrac{(\lambda(t-s))^k}{k!} = \exp(\lambda(t-s)) \]
定义第一条,即一阶矩略了。
现计算\(E\left( \mathbb{X}(t) \mathbb{X(s)} \right)\),设\(P_1=P(\left[ s,t \right], \text{even})\)是信号在两个时刻之间切变偶数次的概率,\(P_{-1}=P(\left[ s,t \right], \text{odd})\)是信号在两个时刻之间切变奇数次的概率,则 \[ E\left( \mathbb{X}(t) \mathbb{X(s)} \right) = 1\cdot P_1 + (-1) \cdot P_{-1} \] 显然,\(P_{-1} = 1-P_1\),因此计算其中一个就行了。现计算 \[ P_1 = \sum_{k:\text{even}} \cfrac{(\lambda(t-s))^k}{k!}\exp(-\lambda(t-s)) \] 利用\(\sum_{k=0}^{\infty} \cfrac{(\lambda(t-s))^k}{k!} = \exp(\lambda(t-s))\)这一关系,注意到,当\(\lambda\)变为\(-\lambda\)时,左边级数中,偶数项值不变,奇数项会变号,右边结果变为\(\exp(-\lambda(t-s))\),于是 \[ \begin{eqnarray} \sum_{k: \text{even}}^{\infty} \cfrac{(\lambda(t-s))^k}{k!} & = & \cfrac{1}{2} \left(\sum_{k=0}^{\infty} \cfrac{(\lambda(t-s))^k}{k!} + \sum_{k=0}^{\infty} \cfrac{(-\lambda(t-s))^k}{k!}\right) \\ & = & \cfrac{1}{2} \left( \exp(\lambda(t-s)) + \exp(-\lambda(t-s)) \right) \end{eqnarray} \] 故 \[ \begin{eqnarray} P_1 & = & \sum_{k:\text{even}} \cfrac{(\lambda(t-s))^k}{k!}\exp(-\lambda(t-s)) \\ & = & \cfrac{1}{2} \left( \exp(\lambda(t-s)) + \exp(-\lambda(t-s)) \right) \exp(-\lambda(t-s)) \\ & = & \cfrac{1}{2} \left( 1 + \exp(-2\lambda(t-s)) \right) \\ \\ P_{-1} & = & \cfrac{1}{2} \left( 1 - \exp(-2\lambda(t-s)) \right) \end{eqnarray} \] 于是 \[ \begin{eqnarray} R_\mathbb{X} (t,s) & = & E\left( \mathbb{X}(t) \mathbb{X(s)} \right)\\ & = & \exp(-2\lambda(t-s))\\ & = & \exp(-2\lambda \tau)) \end{eqnarray} \]
因此,随机过程\(\mathbb{X}\)是宽平稳的。
正定性
一般情况下,相关函数有这样的性质:
- 对称性:\(R_\mathbb{X}(t,s) = R_\mathbb{X}(s, t)\)
- 柯西不等式:\(\left| R_\mathbb{X}(t,s) \right| \leq \left(R_\mathbb{X}(t,t) R_\mathbb{X}(s,s)\right)^\frac{1}{2}\)
对于宽平稳过程\(\mathbb{X}\),由于\(R_\mathbb{X}(s,t) = R_\mathbb{X}(\tau),\ \tau = t-s\),上面两条性质则以表述为:
- 偶函数:\(R_\mathbb{X}(\tau) = R_\mathbb{X}(-\tau)\)
- \(\tau = 0\)为极大值点:\(\left| R_\mathbb{X}(\tau) \right| \leq R_\mathbb{X}(0)\)
除此之外,宽平稳过程的相关函数还有一个非常重要的性质,那就是正定性(positive definite)。首先介绍正定性的概念:
若函数\(f(x)\)满足:
\(\forall n, \forall x_1, x_2, \cdots x_n\),构成矩阵 \[ A_{n\times n} = \left(f(x_i - x_j)\right)_{ij} \] 且这样的\(A_{n\times n}\)是正定的。
则称函数\(f(x)\)是正定的。
矩阵正定有很多种表述,其中一种就是:
矩阵\(A\in \mathbb{R}^{n\times n} \geq0 \Leftrightarrow \forall \alpha \in \mathbb{R}^n, \alpha ^ \mathrm{T}A\alpha \geq 0\)
下面证明宽平稳的相关函数是正定的:
对于宽平稳过程\(\mathbb{X}(t)\),按照定义给出的构造\(R_{n\times n} = \left(R_\mathbb{X}(\tau_i - \tau_j)\right)_{ij}\),任取向量\(\alpha\in\mathbb{R}^n, \alpha = (\alpha_1, \alpha_2, \cdots \alpha_n)^\mathrm{T}\),有
\[ \begin{eqnarray} \alpha^\mathrm{T} R \alpha & = & \left( \begin{array}{} \alpha_1 & \alpha_2 & \cdots &\alpha_n \end{array} \right) \left[ \begin{array}{} R_\mathbb{X}(\tau_1-\tau_1) & R_\mathbb{X}(\tau_1-\tau_2) & \cdots & R_\mathbb{X}(\tau_1-\tau_n) \\ R_\mathbb{X}(\tau_2-\tau_1) & R_\mathbb{X}(\tau_2-\tau_2) & \cdots & R_\mathbb{X}(\tau_2-\tau_n) \\ \vdots & \vdots & \ddots & \vdots \\ R_\mathbb{X}(\tau_n-\tau_1) & R_\mathbb{X}(\tau_n-\tau_2) & \cdots & R_\mathbb{X}(\tau_n-\tau_n) \\ \end{array} \right] \left( \begin{array}{} \alpha_1 \\ \alpha_2 \\ \vdots \\ \alpha_n \end{array} \right) \\ & = & \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j R_\mathbb{X}(\tau_i - \tau_j) \\ & = & \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j E\left( \mathbb{X}(\tau_i) \mathbb{X}(\tau_j) \right) \\ & = & E\left( \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j \mathbb{X}(\tau_i) \mathbb{X}(\tau_j) \right) \\ & = & E\left( \left( \sum_{i=1}^n \alpha_i \mathbb{X}(\tau_i) \right)^2 \right) \\ & \geq & 0 \end{eqnarray} \]
即\(R\)是正定的,因此宽平稳过程\(\mathbb{X}(t)\)是正定的。
这里的计算过程也可以用矩阵-向量语言来更简洁地表述: 令\(\mathbb{X} = (\mathbb{X}(\tau_1), \mathbb{X}(\tau_2), \cdots \mathbb{X}(\tau_n))^\mathrm{T}\),则\(R = \left(R_\mathbb{X}(\tau_i - \tau_j)\right)_{ij} = E(\mathbb{X}\mathbb{X}^\mathrm{T})\),进而 \[ \begin{eqnarray} \alpha^\mathrm{T} R \alpha &=& \alpha^\mathrm{T} E(\mathbb{X}\mathbb{X}^\mathrm{T}) \alpha \\ &=& E\left(\alpha^\mathrm{T} \mathbb{X}\mathbb{X}^\mathrm{T} \alpha\right) \\ &=& E\left((\alpha^\mathrm{T} \mathbb{X})^2 \right) \\ &\geq& 0 \end{eqnarray} \] 这里的\(E(\mathbb{X}\mathbb{X}^\mathrm{T})\)称作相关矩阵(correlation matrix)。
实际上,正定函数\(f(x)\)本身就有非常良好的性质,如
\(f(0)\geq 0\)
证明: 取\(n=1, \forall x_1\),按照定义给出的矩阵: \[ A_{1\times 1} = f(x_1 - x_1) = f(0) \] 由定义可知,\(A\)是正定的,此时即\(f(0)\geq0\),证毕。
\(\forall x, f(0)\geq f(x)\)
证明: 取\(n=2, x_1=0, \forall x_2=x\),按照定义给出的矩阵: \[ A_{2\times 2} = \left[ \begin{array}{} f(0 - 0) & f(0 - x) \\ f(x - 0) & f(x - x) \end{array} \right] = \left[ \begin{array}{} f(0) & f(-x) \\ f(x) & f(0) \end{array} \right] \] 由定义可知,\(A\)是正定的,因此有
\(A\)是对称的,即\(f(-x_2) = f(x_2)\),即\(f\)是偶函数;
\(\det A \geq 0\),即\(\left(f(0)\right)^2 - \left(f(x)\right)^2 \geq 0\),又根据上一条性质\(f(x)\geq0\),有\(f(0) \geq f(x)\),证毕。
可以看出,对于宽平稳过程的相关函数,正定性这一性质实际上包含了上面说明的两条宽平稳过程相关函数的前两条性质。
实际上,正定性是宽平稳过程相关函数的特征性质(characteristic property),也就是说它们是充分必要的关系。
不仅如此,由于正定性,宽平稳过程相关函数\(R_\mathbb{X}(\tau)\)还有其他不平凡的性质,下面我们举几个例子。
周期震荡
前面说到,\(R_\mathbb{X}(0) \geq \left| R_\mathbb{X}(\tau) \right|\),其图像可以感性地表示为:
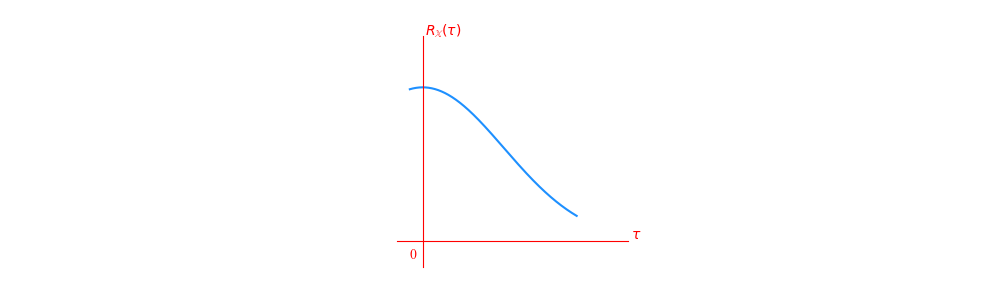
在这样地前提下,若\(\exists T\),满足\(R_\mathbb{X}(T) = R_\mathbb{X}(0)\),则一定有\(R_\mathbb{X}(\tau) = R_\mathbb{X}(\tau+T)\),即\(R_\mathbb{X}\)一定是周期为\(T\)的周期函数。

要证明这一结论,我们想到 \[ \begin{eqnarray} R_\mathbb{X}(\tau) - R_\mathbb{X}(\tau+T) &=& E\left( \mathbb{X}(0)\mathbb{X}(\tau) \right) - E\left( \mathbb{X}(0)\mathbb{X}(\tau + T) \right) \\ &=& E\left( \mathbb{X}(0) \left( \mathbb{X}(\tau) - \mathbb{X}(\tau + T) \right)\right) \end{eqnarray} \] 联系到柯西不等式, \[ \left| E\left( \mathbb{X}(0) \left( \mathbb{X}(\tau) - \mathbb{X}(\tau + T) \right)\right) \right| \leq \left(E\left( \mathbb{X}(0) ^2\right) E\left( \left(\mathbb{X}(\tau) - \mathbb{X}(\tau + T)\right)^2 \right)\right)^\frac{1}{2} \] 如果不等式右边可以证明为\(0\),那么该命题便成立了。按照这样的思路,要证明上面的结论,可以先证明这样的结论:
- 若\(\exists T\),满足\(R_\mathbb{X}(T) = R_\mathbb{X}(0)\),则\(E\left( \left|\mathbb{X}(\tau) - \mathbb{X}(\tau + T)\right|^2 \right)\)。实际上,这一结论称均方周期性。
进而根据柯西不等式得到我们所要的结论。
证明: \[ \begin{eqnarray} E\left( \left|\mathbb{X}(\tau) - \mathbb{X}(\tau + T)\right|^2 \right) &=& E\left( \mathbb{X}(\tau)^2 \right) - 2E\left( \mathbb{X}(\tau) \mathbb{X}(\tau + T) \right) + E\left( \mathbb{X}(\tau + T)^2 \right) \\ &=& E\left( R_\mathbb{X}(0) \right) - 2E\left( R_\mathbb{X}(T) \right) + E\left( R_\mathbb{X}(0) \right) \\ &=& 2\left( R_\mathbb{X}(0) - R_\mathbb{X}(T) \right) \\ &=& 0 \end{eqnarray} \] 故有 \[ \begin{eqnarray} \left| R_\mathbb{X}(\tau) - R_\mathbb{X}(\tau+T) \right| &=& \left| E\left( \mathbb{X}(0) \left( \mathbb{X}(\tau) - \mathbb{X}(\tau + T) \right)\right) \right| \\ &\leq& \left|E\left( \mathbb{X}(0) ^2\right) E\left( \left(\mathbb{X}(\tau) - \mathbb{X}(\tau + T)\right)^2 \right)\right|^\frac{1}{2} \\ &=& 0 \end{eqnarray} \] 因此,\(R_\mathbb{X}(\tau + T) = R_\mathbb{X}(\tau)\),证毕。
Bochner定理
仔细思考上面一节的内容,可以发现是一个“局部性质导出全局性质”的过程。本节继续介绍另一种同样是“局部性质导出全局性质”的过程。
先思考是否存在这样一种矩形窗宽平稳相关函数: \[
R_{\mathbb{X}}(\tau) =
\left\{
\begin{eqnarray}
a && ,\left| \tau \right| <\tau_0 \\
0 && ,\text{elsewhere}
\end{eqnarray}
\right.
(a>0)
\] 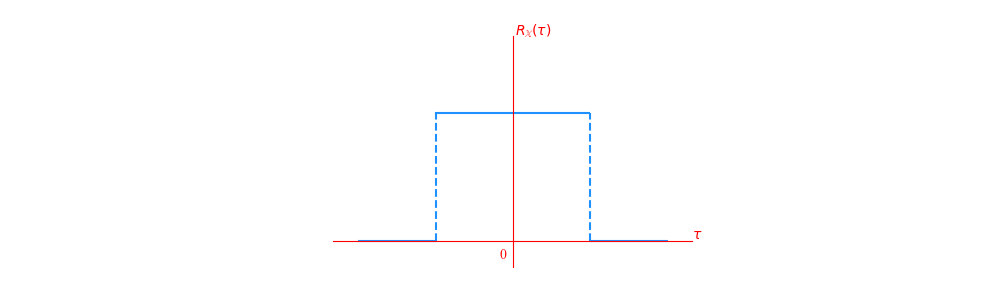
先给出这样命题:
\(R_{\mathbb{X}}(\tau)\)是宽平稳过程的相关函数,若\(R_{\mathbb{X}}(\tau)\)在\(\tau=0\)处连续,则\(R_{\mathbb{X}}(\tau)\)在\(\tau=t, \forall t\)处连续。
若上述命题成立,则显然不存在那样的矩形窗宽平稳相关函数。现在我们就来证明这个命题。
按照上一小节的经验,我们同样把证明过程分解为两部分:
均方连续性:\(R_{\mathbb{X}}(\tau)\)是宽平稳过程的相关函数,若\(R_{\mathbb{X}}(\tau)\)在\(\tau=0\)处连续,则有 \[ \lim_{\Delta\rightarrow0}E\left( \mathbb{X}(t+\Delta) - \mathbb{X}(t) \right)^2 = 0 \]
若一宽平稳随机过程\(\mathbb{X}(t)\)满足上述均方连续性,则其相关函数\(R_{\mathbb{X}}(\tau)\)在\(\tau=t, \forall t\)处连续。
证明:
- \[ E\left( \mathbb{X}(t+\Delta) - \mathbb{X}(t) \right)^2 = 2R_{\mathbb{X}}(0) - 2R_{\mathbb{X}}(\Delta) \] 由于\(R_{\mathbb{X}}(\tau)\)在\(\tau =0\)处连续,故\(\lim_{\Delta \rightarrow 0}\)